Lösning Vecka 8
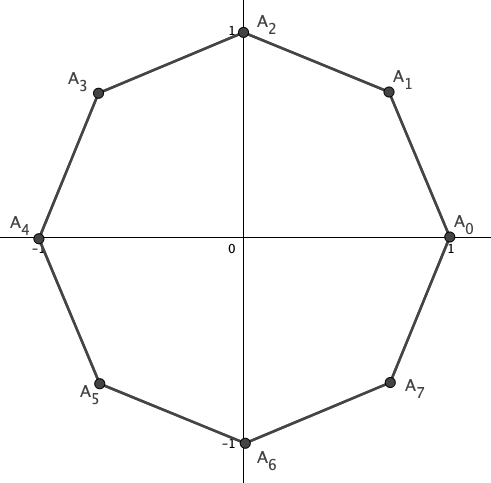
Vi placerar vår n-hörning i det komplexa talplanet så att dess centrum hamnar i origo och ett av hörnen hamnar på punkten $1$, som på bilden nedan. Om vi låter $\omega = e^{\frac{2\pi i}{n}}$ så kommer punkt $A_k$ att vara $\omega^k$. Så längden av $A_0A_k$ kommer bli $|1 - \omega^k|$, eftersom $A_0$ är i punkten $1$. Detta ger att produkten vi vill räkna ut är $|(1 - \omega)(1 - \omega^2)…(1 - \omega^{n-1})|$. Men $\omega^k$ är en rot till polynomet $x^n - 1$, eftersom $(\omega^k)^n = (\omega^n)^k = 1^k = 1$. Vidare har detta polynom exakt $n$ rötter enligt algebrans fundamentalsats, så det måste vara exakt de rötterna. Vi kan enligt faktorsatsen dra slutsatsen att $(x - 1)(x - \omega)(x - \omega^2)…(x - \omega^{n-1}) = x^n - 1$, eftersom $x^n$-koefficienten är ett på båda sidor. Därför blir $(x - \omega)(x - \omega^2)…(x - \omega^{n-1}) = \dfrac{x^n - 1}{x - 1} = x^{n-1} + x^{n-2} + … + x + 1$. Sätter vi in $x = 1$ får vi $(1 - \omega)(1 - \omega^2)…(1 - \omega^{n-1}) = 1^{n-1} + 1^{n-2} + … + 1 = n$, vilket var vad vi skulle visa.
Denna lösning kräver att man kan en del om komplexa tal. Om du inte har hört talas om det innan finns det massor att läsa om det på nätet! Till exempel här. Klicka vidare till Complex plane, De Moivre’s Theorem, Exponential form och Roots of unity för att lära dig allt du behöver för att förstå lösningen ovan.
Bonusproblem (tack till Nils Gustafsson som föreslog detta):
Visa att om vi väljer en punkt $M$ som mittpunkten på cirkelbågen mellan $A_0$ och $A_1$, på den omskrivna cirkeln till n-hörningen, så kommer $|XA_0||XA_1|…|XA_{n-1}| = 2$. (Ledtråd: försök använda samma idé med komplexa tal som i lösningen ovan!).
Gå tillbaka till uppgiften här.