Lösning Vecka 1
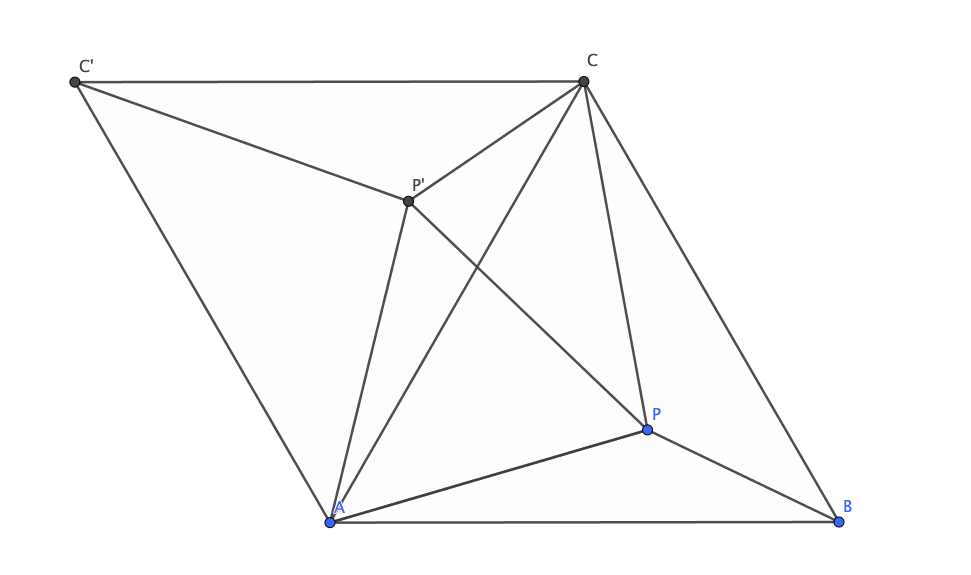
Vi roterar hela triangeln samt punkten \(P\) med \(60^{\circ}\) runt punkten \(A\), så att \(B\), \(C\) och \(P\) hamnar på punkterna \(B’ = C\), \(C’\) respektive \(P’\) (se bild). Vi ser direkt att \(P'P + P’C \geq PC\) enligt triangelolikheten. Men \(P’C = PB\) eftersom det är bilden av \(PB\) efter rotation. Och triangeln \(APP’\) är liksidig eftersom segmentet \(AP’\) är \(AP\) roterat \(60^{\circ}\) kring \(A\), så \(P’P = PA\). Alltså är \(PA + PB \geq PC\), vilket skulle visas!
Likhet får vi precis om \(P, P’\) och \(C\) ligger på en linje, och \(P’\) ligger mellan \(P\) och \(C\). I så fall är \(\angle APC = \angle APP’\), som i sin tur är lika med \(60^{\circ}\) eftersom \(\triangle APP’\) är liksidig. Alltså är \(\angle APC = 60^{\circ} = \angle ABC\), så enligt randvinkelsatsen ligger \(P\) på omskrivna cirkeln till \(\triangle ABC\). \(P\) måste dessutom ligga på den korta bågen mellan \(A\) och \(B\) för att vi ska ha likheten i uppgiften (rita en bild om du är osäker! Det finns lite olika konfigurationer som måste hanteras separat om man ska vara noga.)
Gå tillbaka till uppgiften här.